Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T06:59:59.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Verifying non-isomorphism of groups

Published online by Cambridge University Press:  13 October 2021

Des MacHale
Des MacHale*
Affiliation:
School of Mathematics, Applied Mathematics and Statistics, University College Cork, Cork, Ireland, e-mail: d.machale@ucc.ie
Get access Rights & Permissions [Opens in a new window]

Extract

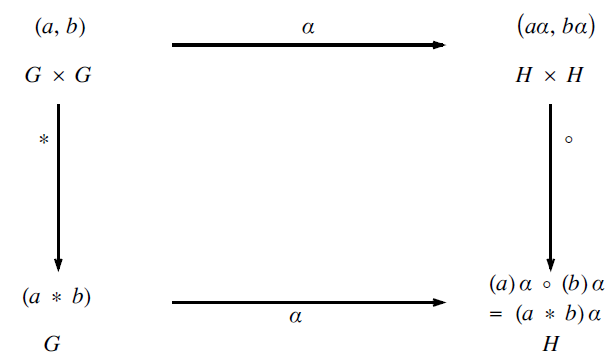
The concept of isomorphism is central to group theory, indeed to all of abstract algebra. Two groups {G, *} and {H, ο}are said to be isomorphic to each other if there exists a set bijection α from G onto H, such that 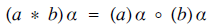$$\left( {a\;*\;b} \right)\alpha = \left( a \right)\alpha \; \circ \;(b)\alpha $$ for all a, b ∈ G. This can be illustrated by what is usually known as a commutative diagram:

Type
Articles
Information
The Mathematical Gazette , Volume 105 , Issue 564 , November 2021 , pp. 467 - 473
Check for updates
Copyright
© The Mathematical Association 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

MacDonald, I. D., Theory of Groups, Oxford (1968).Google Scholar
Herstein, I. N., Topics in Algebra, Wiley (2013).Google Scholar
Frobenius, F. G., Uber die Darstellung der endlichen Gruppen dursch lineare substitutionen, Sitz. Kon. Preuss. Acad. Wiss. Berlin (1897) pp. 944-1015.Google Scholar
Formanek, E. and Sibley, D., The Group Determinant determines the group, Proc. Amer. Math. Soc. 112 (3) (1991) pp. 649-656.CrossRefGoogle Scholar