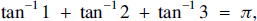No CrossRef data available.
Published online by Cambridge University Press: 21 October 2019
Andrew Palfreyman’s article [1] reminds us of the result
(1)$${\rm{ta}}{{\rm{n}}^{{\rm{ - 1}}}}{\rm{ + ta}}{{\rm{n}}^{{\rm{ - 1}}}}\,2{\rm{ + ta}}{{\rm{n}}^{{\rm{ - 1}}}}{\rm{ 3 = }}\,\pi {\rm{, }}$$
having been set the challenge of finding the value of the left-hand side by his head of department at the start of a departmental meeting.