No CrossRef data available.
Article contents
An Algebraic Theorem Related to the Theory of Relativity
Published online by Cambridge University Press: 03 November 2016
Extract
In a common development of the special theory of relativity one considers two events P and Q, P being the emission of a flash of light and Q the reception of the light. We suppose Q to be infinitesimally close to P and, by using the principle of the invariance of c, the velocity of light, argue that the infinitesimal coordinate differences between P and Q must satisfy
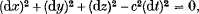 Iand
Iand
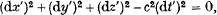 II
II
where dx; etc. are the coordinate differences in one inertial frame whilst dx' etc. are those in a second inertial frame (e.g. [1], p. 16).
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1972


