Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T07:29:49.461Z Has data issue: false hasContentIssue false
  • English
  • Français

Archimedes playing with a computer

Published online by Cambridge University Press:  12 October 2022

François Dubeau
François Dubeau*
Affiliation:
Département de mathématiques, Faculté des sciences, Université de Sherbrooke, 2500 Bd. de l'Université, Sherbrooke (QC), J1K 2R1 Canada e-mail: francois.dubeau@usherbrooke.ca
Get access Rights & Permissions [Opens in a new window]

Extract

It was known before Archimedes (287-212 BC) that the circumference of a circle was proportional to its diameter and that the area was proportional to the square of its radius. It was Archimedes who first supplied a rigorous proof that these two proportionality constants were the same, now called π [1]. He started with inscribed and circumscribed hexagons and increased the number of sides from 6 up to 96 by successively doubling it. His result was not a single value. In fact he generated five intervals each of which contained π. He calculated a lower bound from the inscribed polygon and an upper bound from the circumscribed polygon of 96 sides. This gave him the interval (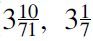) or (3.140845, 3.142857), which is less accurate than the interval bounded by half-perimeters of the inscribed and circumscribed 96-gons, which is (3.141031, 3.142714).

Type
Articles
Information
The Mathematical Gazette , Volume 106 , Issue 567 , November 2022 , pp. 427 - 442
Check for updates
Copyright
© The Authors, 2022. Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Edwards, C. H. Jr., The historical development of the calculus, Springer-Verlag (1979).Google Scholar
Kincaid, D. and Cheney, W., Numerical Analysis, Brooks/Cole (1991).Google Scholar
Joyce, D. C., Survey of extrapolation processes in numerical analysis, SIAM Review, 13(4) (1971) pp. 435–490.Google Scholar
Slowbe, J., What if Archimedes had met Taylor?, Mathematics Magazine, 81(4) (2008) pp. 285–290.Google Scholar