Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T07:29:04.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Beyond the Basel problem: Euler’s derivation of the general formula for ζ (2n)

Published online by Cambridge University Press:  25 August 2015

Nick Lord
Nick Lord*
Affiliation:
Tonbridge School, Kent TN9 1JP
Get access Rights & Permissions [Opens in a new window]

Extract

The problem of finding a closed-form evaluation of 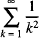baffled the pioneers of calculus such as Leibniz and James Bernoulli and, following the latter’s promulgation of the problem, it became known as the Basel problem after his home town (which was also Euler’s birthplace). Euler’s early sensational success in solving the Basel problem by identifying 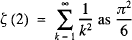is extremely well-documented. In this paper, we give the full details of his subsequent derivation of the general formula

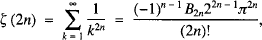(1)

where (Bn) is a sequence of ‘strange constants’. Euler’s polished account of his discovery, in which he popularised the designation of the strange constants as ‘Bernoulli numbers’, appears in Chapter 5 of Volume 2 of his great textbook Institutiones calculi differentialis [1; E212]: see [2] for an online English translation. Here, we will focus on his initial step-by-step account which appeared in his paper with Eneström number E130, written c1739, carrying the rather nondescript title De seriebus quibusdam considerationes, ‘Considerations about certain series’. (For convenience, we will just use ‘Eneström numbers’ when referencing Euler’s work: all are readily available on-line at [1].) Euler’s proof is notable for its early, sophisticated and incisive use of generating functions and for his brilliant insight that the sequence (Bn) occurring in the coefficients of the general ζ(2n) formula (1) also occurs in the Euler-Maclaurin summation formula and in the Maclaurin expansion of 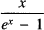. By retracing Euler’s original path, we shall not only be able to admire the master in full creative flow, but also appreciate the role played by recurrence relations such as

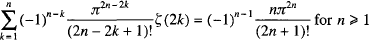(2)

which, as our ample list of references (which will be reviewed later) suggests, have been rediscovered over and over again in the literature. Moreover, our historical approach makes it clear that, while deriving (2) is relatively straightforward (and may be used to calculate ζ(2n) recursively as a rational multiple of π2n), it is establishing the connection between ζ(2n) and the Bernoulli numbers that was for Euler the more difficult step. Even today, this step presents pedagogical challenges depending on one’s starting definition for the Bernoulli numbers and what identities satisfied by them one is prepared to assume or derive.

Type
Research Article
Information
The Mathematical Gazette , Volume 98 , Issue 543 , November 2014 , pp. 459 - 474
Copyright
Copyright © The Mathematical Association 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Mathematical Association of America, The Euler Archive, accessed February 2014 at http://www.math.dartmouth.edu/~euler/ Google Scholar
2. Pengelley, D., Excerpts on the Euler-Maclaurin summation formula (2000) available at http://www.math.nmsu.edu/~davidp/institutionescalcdiff.pdf Google Scholar
3. Lord, N., Intriguing integrals: an Euler-inspired Odyssey, Math. Gaz. 91 (November 2007) pp. 415–427.Google Scholar
4. Weil, A., Number theory: an approach through history, Birkhäuser (1984) pp. 256–272.Google Scholar
5. Ayoub, R., Euler and the zeta function, Amer. Math. Monthly 81 (1974) pp. 1067–1086.Google Scholar
6. Sandifer, C.E., The MAA Tercentenary Euler Celebration, Volume 1, Math. Assoc. Amer. (2007) pp. 342–348.Google Scholar
7. Varadarajan, V.S., Euler and his work on infinite series, Bull. Amer. Math. Soc. 44 (2007) pp. 513–539.Google Scholar
8. Lord, N., Variations on a theme - Euler and the logsine integral, Math. Gaz. 96 (November 2012) pp. 451–458.Google Scholar
9. Ewell, J.A., A new series representation for ζ (3), Amer. Math. Monthly 97 (1990) pp. 219–220.Google Scholar
10. Durell, C.V. and Robson, A., Advanced trigonometry, Bell (1930) pp. 222–223, 228-229, 240.Google Scholar
11. Ireland, K. and Rosen, M., A classical introduction to modern number theory, Springer (1982) pp. 228–232.Google Scholar
12. Aigner, M. and Ziegler, G.M., Proofs from The Book (2nd edn.), Springer (2002) Chapter 19.Google Scholar
13. Elkies, N.D., On the sums , Amer. Math. Monthly 110 (2003) pp. 561–573.Google Scholar
14. Bényi, Á., Finding the sums of harmonic series of even order, Coll. Math. Journal 36 (2005) pp. 44–48.Google Scholar
15. Osler, T.J. and Zeng, J., Finding ζ(2n) from a recursive relation for Bernoulli numbers, Math. Gaz. 91 (March 2007) pp. 123–126.Google Scholar
16. Murphy, R.V.W., Summing powers of natural numbers, Math. Gaz. 93 (July 2009) pp. 279–285.Google Scholar
17. Hirschhorn, M., Feedback on 93.23, Math. Gaz. 94 (March 2010) pp. 153–154.Google Scholar
18. Khan, R.A., The recursive nature of Euler’s formula for harmonic series, Math. Gaz. 94 (November 2010) pp. 488–492.Google Scholar
19. Robbins, N., Revisiting an old favourite: ζ(2m), Math. Mag. 72 (1999) pp. 317–319.Google Scholar
20. Song, I., A recursive formula for even order harmonic series, J. Comp. Appi. Math. 21 (1988) pp. 251–256.Google Scholar
21. Kuo, H-T., A recurrence formula for ζ(2n), Bull. Amer. Math. Soc. 55 (1949) pp. 573–574.Google Scholar
22. Chen, X., Recursive formula for ζ(2k) and L(2k − 1), Coll. Math. Journal 26 (1995) pp. 372–376.Google Scholar
23. Chungang, Ji & Yonggao, Chen, Euler’s formula for ζ(2k), proved by induction on k , Math. Mag. 73 (2000) pp. 154–155.Google Scholar
24. Stark, E.L., The series once more, Math. Mag. 47 (1974) pp. 197–202.Google Scholar
25. Yue, Z.N. and Williams, K.S., Application of the Hurwitz zeta function to the evaluation of certain integrals, Canadian Math. Bull. 36 (1993) pp. 373–384.Google Scholar
26. Dalai, M., How would Riemann evaluate ζ(2n)?, Amer. Math. Monthly 120 (2013) pp.169–171.Google Scholar
27. Apostol, T.M., Another elementary proof of Euler’s formula for ζ(2n), Amer. Math. Monthly 80 (1973) pp. 425–431.Google Scholar
28. Tsumura, H., An elementary proof of Euler’s formula for ζ(2m), Amer. Math. Monthly 111 (2004) pp. 430–431.Google Scholar
29. Barnard, S. and Child, J.M., Higher algebra, Macmillan (1936).Google Scholar
30. Underwood, R.S., An expression for the summation , Amer. Math. Monthly 35 (1928) pp. 424–428.Google Scholar
31. Berndt, B.C., Elementary evaluation of ζ(2n), Math. Mag. 48 (1975) pp. 148–154.Google Scholar
32. Williams, G.T., A new method of evaluating ζ(2n), Amer. Math. Monthly 60 (1953) pp. 19–25.Google Scholar
33. Boros, G. and Moll, V.H., Irresistible integrals, Cambridge University Press (2004) pp. 100, 220.Google Scholar
34. Estermann, T., Elementary evaluation of ζ(2k), J. London Math. Soc. 22 (1947) pp. 10–13.Google Scholar
35. Bényi, Á., A recursion for alternating harmonic series, J. Appl. Math. & Comp. 18 (2005) pp. 377–381.Google Scholar
35. Whittaker, E.T. and Watson, G.N., A course of modern analysis (4th edn.), Cambridge University Press (1973) pp. 125–128.Google Scholar
37. Dieudonné, J., Mathematics – the music of reason, Springer (1992) pp. 98–101.Google Scholar
38. Apostol, T.M., Mathematical analysis (2nd edn.), Addison-Wesley (1974) p. 251, 338.Google Scholar
39. Bromwich, T.J.T.A., An introduction to the theory of infinite series (2nd edn.), Macmillan (1959) pp. 359–364.Google Scholar
40. Woodhouse, F., The Basel problem and the zeros of , Math. Gaz. 91 (March 2007) pp. 120–123.Google Scholar
41. Lowry, H.V., Elementary derivation of the Euler-Maclaurin summation formula, Math. Gaz. 31 (October 1947) pp. 248–249.Google Scholar
42. CRC standard mathematical tables and formulae (30th edn.), CRC Press (1996), p. 21 (Formula 1.2.7).Google Scholar
43. Vakil, R., A mathematical mosaic, Brendan Kelly Publishing (1996) pp. 138.Google Scholar
44. Sandifer, E., How Euler did it, Mathematical Association of America http://maa.org/news/howeulerdidit.html (September 2005).Google Scholar
45. Pengelley, D., Dances between continuous and discrete: Euler’s summation formula (2002), available at http://www.math.nmsu.edu/~davidp/euler2k2.pdf Google Scholar
46. Apostol, T.M., A primer on Bernoulli numbers and polynomials, Math. Mag. 81 (2008) pp. 178–190.Google Scholar
47. Roy, R., Sources in the development of mathematics: series and products from the 15th to the 21st century, Cambridge University Press (2011).Google Scholar