Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-14T07:31:43.207Z Has data issue: false hasContentIssue false
  • English
  • Français

A Case of Three Rotating Lines and the Point “O.”

Published online by Cambridge University Press:  03 November 2016

Get access Rights & Permissions [Opens in a new window]

Extract

1. Let AP, BQ, CR be three lines through the vertices of the ΔABC which rotate with equal angular velocity ω, and which make equal angles with the opposite sides, the initial position being that of the three altitudes of ABC. Then the three circles AQR, BRP, CPQ, which meet in the well-known point O, will be shewn to form three coaxal systems; and among other things we shall shew that the locus of O is the circle on GH as diameter, G being the centroid and H the orthocentre.

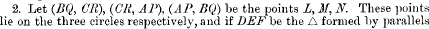
Type
Research Article
Information
The Mathematical Gazette , Volume 6 , Issue 101 , December 1912 , pp. 392 - 394
Copyright
Copyright © Mathematical Association 1912 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)