Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T07:26:44.531Z Has data issue: false hasContentIssue false
  • English
  • Français

A Catalan constant inspired integral odyssey

Published online by Cambridge University Press:  08 October 2020

Seán M. Stewart
Seán M. Stewart*
Affiliation:
9 Tanang Street, Bomaderry, NSW, 2541, Australia e-mail: sean.stewart@physics.org
Get access Rights & Permissions [Opens in a new window]

Extract

There is a rich and seemingly endless source of definite integrals that can be equated to or expressed in terms of Catalan's constant. Denoted by G and defined by

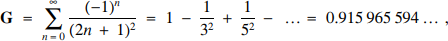$${\rm{G}} = \sum\limits_{n = 0}^\infty {{{{{\left( { - 1} \right)}^n}} \over {{{\left( {2n + 1} \right)}^2}}} = 1 - {1 \over {{3^2}}} + {1 \over {{5^2}}} \ldots = 0.915\,965\,594 \ldots \,\,,} $$
Scott in [1] quipped that this constant seemed almost as useful as the more widely known Euler–Mascheroni constant γ, particularly in the evaluation of definite integrals. And like γ, Catalan's constant continues to remain one of the most inscrutable constants in mathematics where the question concerning its irrationality is not settled.

Type
Articles
Information
The Mathematical Gazette , Volume 104 , Issue 561 , November 2020 , pp. 449 - 459
Check for updates
Copyright
© Mathematical Association 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Scott, J. A., In praise of the Catalan constant, Math. Gaz. 86 (March 2002) pp. 102–103.10.2307/3621589CrossRefGoogle Scholar
Adamchik, Victor, 33 representations for Catalan's constant, Carnegie Mellon University (2000).Google Scholar
Bradley, David M., Representations of Catalan's constant (2001), available at www.researchgate.net/publication/2325473Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M. (eds), Table of integrals, series, and products (8th edn.), Academic Press (2015).Google Scholar
Gröbner, Wolfgang and Hofreiter, Nikolaus (eds), Integraltafel: Zweiter Teil, Bestimmte Integrale (5th edn.), Springer-Verlag (1973).Google Scholar
Jameson, Graham and Lord, Nick, Integrals evaluated in terms of Catalan's constant, Math. Gaz. 101 (March 2017) pp. 38–49.10.1017/mag.2017.4CrossRefGoogle Scholar
Lord, Nick, Variations on a theme – Euler and the logsine integral, Math. Gaz. 96 (November 2012) pp. 451–458.CrossRefGoogle Scholar
Stewart, Seán M., How to integrate it: a practical guide to finding elementary integrals, Cambridge University Press (2018).Google Scholar
Bierens de Haan, D., Nouvelles tables d'intégrales définies, P. Engels (1867).Google Scholar
Ioan, Cornel, Problem 12107, Amer. Math. Monthly 126 (April 2019) p. 370.Google Scholar