Composition of polynomials

Extract

The motivation to write this paper arose out of the following problem which was posed in a recent mathematical olympiad:

Given a polynomial P(X) with integer coefficients, show that there exist non-zero polynomials Q(X), R(X) with integer coefficients such that P(X)Q(X) is a polynomial in X² and P(X)R(X) is a polynomial in X³.

For instance, if P(X) = 2 − 5X + 3X² + 12X³, then we notice that Q (X) = 2 + 5X + 3X² − 12X³ serves the purpose for the first part, viz.

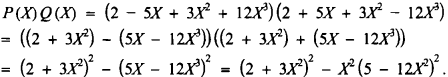
A moment's thought makes it fairly evident that this trick easily solves the first part of the problem for a general polynomial P(X).