Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-11T04:45:53.175Z Has data issue: false hasContentIssue false
  • English
  • Français

Defining trigonometric functions via complex sequences

Published online by Cambridge University Press:  14 March 2016

Jan Gustavsson  and
Mikael P. Sundqvist
Jan Gustavsson
Affiliation:
Lund University, Department of Mathematical Sciences, Box 118, 221 00 Lund, Swedene-mail:jang@maths.lth.se; mickep@maths.lth.se
Mikael P. Sundqvist
Affiliation:
Lund University, Department of Mathematical Sciences, Box 118, 221 00 Lund, Swedene-mail:jang@maths.lth.se; mickep@maths.lth.se
Get access Rights & Permissions [Opens in a new window]

Extract

In the literature we find several different ways of introducing elementary functions. For the exponential function, we mention the following ways of characterising the exponential function:

(a)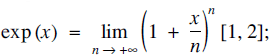

(b) 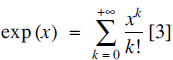, also for complex values of x;

(c) x → exp (x) is the unique solution to the initial value problem [4]

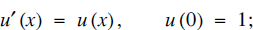
(d) x → exp (x) is the inverse of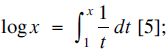

(e)x → exp (x) is the unique continuous function satisfying the

functional equation f (x + y) = f (x) f (y) and f(0) = 1 [6]; the corresponding definition is done for the logarithm in [7];

(f) Define dr for rational r, and then use a continuity/density argument [8].

All of them have their advantages and disadvantages. We like (a) and (c), mostly because they have natural interpretations, (a) in the setting of compound interest and (c) being a simple model of many processes in physics and other sciences, but also because they are related to methods and ideas that are (usually) introduced rather early to the students.

Type
Research Article
Information
The Mathematical Gazette , Volume 100 , Issue 547 , March 2016 , pp. 9 - 23
Copyright
Copyright © Mathematical Association 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Melzak, Z. A., On the exponential function, Amer. Math. Monthly, 82 (8), (October 1975) pp. 842–844.CrossRefGoogle Scholar
2.Euler, Leonhard, Introduction to analysis of the infinite, Book I, Springer-Verlag, New York (1988). Translated from the Latin by Blanton, John D..Google Scholar
3.Rudin, Walter, Principles of mathematical analysis (3rd edn.) McGraw-Hill (1976).Google Scholar
4.Diamond, Harvey, Defining exponential and trigonometric functions using differential equations, Mathematics Magazine, 87 (1), (February 2014) pp. 37–42.CrossRefGoogle Scholar
5.Apostol, Tom M., Calculus, Vol. I: One-variable calculus, with an introduction to linear algebra (2nd edn.) Blaisdell Publishing Co., Waltham, Mass. (1967).Google Scholar
6.Cauchy, Augustin-Louis, Cours d'analyse de I'École Royale Poly technique, Cambridge Library Collection, Cambridge University Press, Cambridge (2009).CrossRefGoogle Scholar
7.Dieudonné, J., Foundations of modern analysis, Academic Press (1969).Google Scholar
8.Courant, Richard and John, Fritz, Introduction to calculus and analysis, Vol. I, Springer-Verlag, New York (1965).Google Scholar
9.Adams, R. A., Calculus: A complete course, Addison-Wesley (1995).Google Scholar
10.Rosenlicht, Maxwell, Introduction to analysis. Dover Publications (1986).Google Scholar
11.Kearns, D. A., An analytic approach to trigonometric Functions, Amer. Math. Monthly, 65(8) (1958) pp. 616–620.Google Scholar
12.Cooper, R., The exponential and logarithmic functions, Math. Gaz., 20 (October 1936) pp. 258–263.CrossRefGoogle Scholar
13.Arnold, Vladimir I., Ordinary differential equations, Universitext, Springer-Verlag, Berlin (2006). Translated from the Russian by Cooke, Roger.Google Scholar
14.Åkerberg, Bengt, A proof of the arithmetic-geometric mean inequality, Amer. Math. Monthly, 70 (9) (November 1963) p. 997.Google Scholar