Derangement revisited

Extract

In [1], the following theorem is stated and proved as Proposition XXXII, using the Principle of Inclusion and Exclusion:

The number of ways of deranging a series of n terms so that no term may be followed by the term which originally followed it is

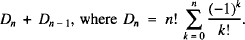
(Note that the conventional definition of a derangement of a series of terms is an arrangement such that no term occupies its original position. However, the usage in this paper allows some terms to remain in their original positions.) This may most easily be visualised by considering a string of n distinct characters, abc … n say. This string has a sequence of n − 1 pairs of consecutive characters, namely, ab, bc, … mn. This article derives three theorems that can be deduced from the above theorem. The first theorem determines the number of permutations of a character string that are free from a random subset comprising a given number m of the n − 1 pairs, but contain all the remaining pairs. The second theorem sums the results of the first theorem for m, m + 1, …, n − 1 pairs.