A Descriptive Proof of a Theorem for Conic Sections

Extract

1 To prove that a line meeting one given conic in points harmonic to its intersections with another given conic, touches a conic.

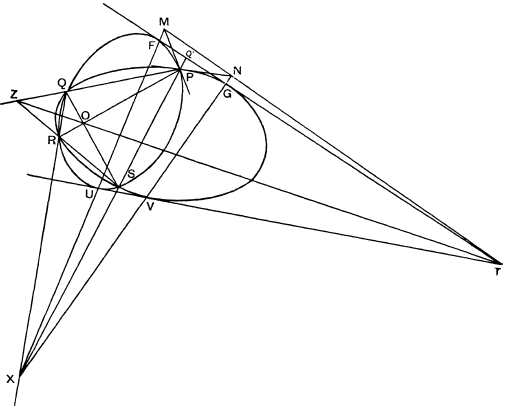
2. Lemma I. Let two conies intersect in P, Q, R, S as shown in Fig. 1.

Let UV, FG be a pair of common tangents intersecting in T, and let the tangents at P to the two conies cut UF, VG in the points M, N respectively. Then M, N, T are collinear

For: QR, PS, FU, GV all meet in a point X, and the range MFUX is related to the pencil P(PFUS), which is related to F(PFUS), which is related to PQ′XS, where Q′ is the intersection of SP and FG Similarly, NGVX is related to PQ′XS. Hence MFUX and NGVX are related, and thus MN passes through T