No CrossRef data available.
Article contents
Determinant Expansions
Published online by Cambridge University Press: 03 November 2016
Extract
A Set of numbers aij (called elements) arranged in a rectangular array of m rows and n columns constitutes a matrix of orders m × n. For example, of the arrays
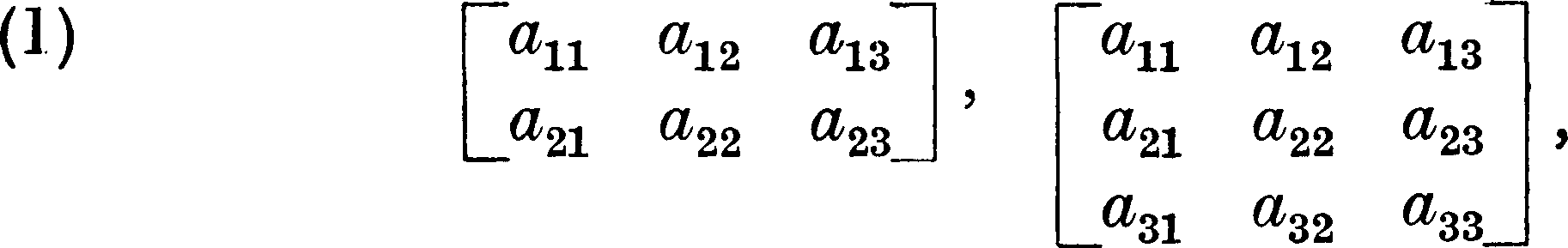
the first is a matrix of two rows and three columns, i.e. of orders 2 × 3, the second is a square matrix of orders 3 × 3.
From a square matrix of orders n × n we can form a determinant of order n. Thus from the above square matrix we can form the determinant of order 3
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1941
References
page no 132 note * Rice, L. H. (American Jour. of Math. 42, p. 237 (1920))CrossRefGoogle Scholar. This remarkable and general theorem appears to have been overlooked by writers on determinants.
page no 134 note * Albeggiani, M. (Giornale di Mat., 13, p. 1 (1874))Google Scholar. The proof which follows is due to Rice, loc. cit.

