No CrossRef data available.
Article contents
A diagram for inequalities of symmetric functions
Published online by Cambridge University Press: 21 October 2019
Extract
Consider the problem of proving that, for any positive numbers x, y and z,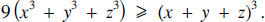 $${\rm{9 (}}{{\rm{x}}^{\rm{3}}}{\rm{+}}{{\rm{y}}^{\rm{3}}}{\rm{+}}{{\rm{z}}^{\rm{3}}}{\rm{) }} \ge {\rm{ (x+y+z}}{{\rm{)}}^{\rm{3}}}{\rm{ }}{\rm{.}}$$
$${\rm{9 (}}{{\rm{x}}^{\rm{3}}}{\rm{+}}{{\rm{y}}^{\rm{3}}}{\rm{+}}{{\rm{z}}^{\rm{3}}}{\rm{) }} \ge {\rm{ (x+y+z}}{{\rm{)}}^{\rm{3}}}{\rm{ }}{\rm{.}}$$
This is an example of a type of inequality that frequently occurs in Olympiad-style problems, [1]. These problems may involve symmetric functions of more or fewer variables than the three used here. However, three variables are commonly used and appear to give appropriately difficult problems without making excessive computational demands.
Information
- Type
- Articles
- Information
- Copyright
- © Mathematical Association 2019
References
The Art of Problem Solving, Mildorf Inequalities, accessed June 2019, at https://artofproblemsolving.com/articles/files/MildorfInequalities.pdf
Google Scholar
Wikipedia, Schur’s inequality (2018), available at https://en.wikipedia.org/wiki/Schur%27s_inequality
Google Scholar

