Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T07:35:20.116Z Has data issue: false hasContentIssue false
  • English
  • Français

A digit function with Thomae-like properties

Published online by Cambridge University Press:  23 January 2015

Martin Griffiths
Martin Griffiths*
Affiliation:
Department of Mathematical Sciences, University of Essex, Colchester CO4 3SQ
Get access Rights & Permissions [Opens in a new window]

Extract

Following a recent revival of interest in both Thomae's function and digit functions (see [1] and [2] respectively) we present here a function providing an appealing link between the two. The former, nowadays often cited in courses on real analysis, was given by Thomae in 1875; see also [3], [4] and [5]. This function, which we denote by g(x), has the following definition:

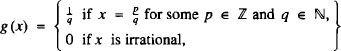
where it is so be assumed that gcd (p, q) = 1 when x is rational.

Type
Articles
Information
The Mathematical Gazette , Volume 95 , Issue 534 , November 2011 , pp. 397 - 403
Copyright
Copyright © The Mathematical Association 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Beanland, K., Roberts, J. W., and Stevenson, C., Modification of Thomae's function and differentiability, Amer. Math. Monthly 116 (2009) pp.531–535.Google Scholar
2. Simons, S., Summing digits of an arithmetic sequence, Math. Gaz. 92 (2008) pp. 83–86.Google Scholar
3. Abbott, S., Understanding analysis, Springer (2001) p. 102.Google Scholar
4. Wikipedia: The Free Encyclopedia, Thomae's function, http://en.wikipedia.org/wiki/Thomae's_function Google Scholar
5. Wilcox, H. J. and Myers, D. L., An introduction to Lebesgue integration and Fourier series, Dover (1995) p. 8.Google Scholar
6. Drmota, M. and Gaidosik, J., The distribution of the sum-of-digits function, Journal de Théorie des Nombres de Bordeaux 10 (1998) pp.17–32.Google Scholar
7. Kirschenhofer, P., On the variance of the sum of digits function, Lecuture Notes Math. 1452 (1990) pp.112–116.Google Scholar
8. Apostol, T. M., Mathematical analysis (2nd edn.), Addison Wesley (1974).Google Scholar