Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-14T07:26:07.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Digit Maps

Published online by Cambridge University Press:  16 February 2023

Niphawan Phoopha ,
Prapanpong Pongsriiam  and
Phakhinkon Napp Phunphayap
Niphawan Phoopha
Affiliation:
Department of Mathematics, Faculty of Science, Silpakorn University, Nakhon Pathom, 73000, Thailand e-mails: phoopha.miw@gmail.com, prapanpong@gmail.com
Prapanpong Pongsriiam
Affiliation:
Department of Mathematics, Faculty of Science, Silpakorn University, Nakhon Pathom, 73000, Thailand e-mails: phoopha.miw@gmail.com, prapanpong@gmail.com
Phakhinkon Napp Phunphayap
Affiliation:
Department of Mathematics, Faculty of Science, Burapha University, Chonburi, 20131 Thailand e-mails: phakhinkon.ph@go.buu.ac.th, phakhinkon@gmail.com
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The happy function S of each positive integer x is defined to be the sum of the squares of the decimal digits of x. For example, S(2) = 4 and S(123) = 12 + 22 + 32 = 14. It is well known that for any 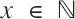, there exists 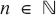such that 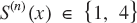, where S(n) is the n-fold composition of S. In addition, if 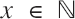and 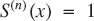for some 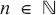, then x is called a happy number.

Type
Articles
Information
The Mathematical Gazette , Volume 107 , Issue 568 , March 2023 , pp. 35 - 43
Check for updates
Copyright
© The Authors, 2023. Published by Cambridge University Press on behalf of The Mathematical Association

References

El-Sedy, E. and Siksek, S., On happy numbers, Rocky Mountain J. Math. 30 (2000) pp. 565–570.CrossRefGoogle Scholar
Grundman, H. G. and Teeple, E. A., Generalized happy numbers, Fibonacci Quart. 39(5) (2001) pp. 462–466.Google Scholar
Guy, R. K., Unsolved problems in number theory (3rd edn.), Springer-Verlag (1981).10.1007/978-1-4757-1738-9_2CrossRefGoogle Scholar
Pan, H., On consecutive happy numbers, J. Number Theory 128 (2008) pp. 1646–1654.CrossRefGoogle Scholar
Zhou, X. and Cai, T., On e-power b-happy numbers, Rocky Mountain J. Math. 39 (2009) pp. 2073–2081.CrossRefGoogle Scholar
Gilmer, J., On the density of happy numbers, Integers 13 (2013), pp. 1–25.Google Scholar
Styer, R., Smallest examples of strings of consecutive happy numbers, J. Integer Seq. 13 (2010), Article 10.6.3.Google Scholar
Chase, Z., On the iterates of digit maps, Integers 18 (2018) pp. 1–7.Google Scholar
Grundman, H. G., Semihappy numbers, J. Integer Seq. 13 (2010), Article 10.4.8.Google Scholar
Swart, B. B., Beck, K. A., Crook, S., Turner, C. E., Grundman, H. G., Mei, M. and Zack, L., Augmented generalized happy functions, Rocky Mountain J. Math. 47 (2017) pp. 403–417.CrossRefGoogle Scholar
Noppakeaw, P., Phoopha, N., and Pongsriiam, P., Composition of happy functions, Notes Number Theory Discrete Math. 25 (2019) pp. 13–20.CrossRefGoogle Scholar
Subwattanachai, K. and Pongsriiam, P., Composition of happy functions and digit maps, Int. J. Math. Comp. Sci. 16(1) (2021) pp. 169–178.Google Scholar
Hargreaves, K. and Siksek, S., Cycles and fixed points of happy functions, J. Comb. Number Theory 2(3) (2010) pp. 65–77.Google Scholar