Article contents
Euler, the clothoid and 
Published online by Cambridge University Press: 14 June 2016
Extract
One of the many definite integrals that Euler was the first to evaluate was
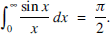 (1)
(1)
He did this, almost as an afterthought, at the end of his short, seven-page paper catalogued as E675 in [1] and with the matter-of-fact title, On the values of integrals from x = 0 to x = ∞. It is a beautiful Euler miniature which neatly illustrates the unexpected twists and turns in the history of mathematics. For Euler's derivation of (1) emerges as the by-product of a solution to a problem in differential geometry concerning the clothoid curve which he had first encountered nearly forty years earlier in his paper E65, [1]. As highlighted in the recent Gazette article [2], E675 is notable for Euler's use of a complex number substitution to evaluate a real-variable integral. He used this technique in about a dozen of the papers written in the last decade of his life. The rationale for this manoeuvre caused much debate among later mathematicians such as Laplace and Poisson and the technique was only put on a secure footing by the work of Cauchy from 1814 onwards on the foundations of complex function theory, [3, Chapter 1]. Euler's justification was essentially pragmatic (in agreement with numerical evidence) and by what Dunham in [4, p. 68] characterises as his informal credo, ‘Follow the formulas, and they will lead to the truth.’ Smithies, [3, p. 187], contextualises Euler's approach by noting that, at that time, ‘a function was usually thought of as being defined by an analytic expression; by the principle of the generality of analysis, which was widely and often tacitly accepted, such an expression was expected to be valid for all values, real or complex, of the independent variable’. In this article, we examine E675 closely. We have tweaked notation and condensed the working in places to reflect modern usage. At the end, we outline what is, with hindsight, needed to make Euler's arguments watertight: it is worth noting that all of his conclusions survive intact and that the intermediate functions of one and two variables that he introduces in E675 remain the key ingredients for much subsequent work on these integrals.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 2016
References
- 2
- Cited by


