No CrossRef data available.
Article contents
Expressions for rational approximations to square roots of integers using Pell's equation
Published online by Cambridge University Press: 14 February 2019
Extract
There are recursive expressions (see [1]) for sequentially generating the integer solutions to Pell's equation: p2 − Dq2 = 1, where D is any positive non-square integer. With known positive integer solution p1 and q1 we can compute, using these recursive expressions, pn and qn for all n > 1. See Table in [2] for a list of smallest integer, or fundamental, solutions p1 and q1 for D≤ 128. These (pn, qn) pairs also form rational approximations to 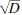 that, as noted in [3, Chapter 3], match with convergents (Cn = pn / qn) of the Regular Continued Fractions (RCF, continued fractions with the numerator of all fractions equal to 1) for
that, as noted in [3, Chapter 3], match with convergents (Cn = pn / qn) of the Regular Continued Fractions (RCF, continued fractions with the numerator of all fractions equal to 1) for 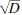 .
.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2019
References
1. Wikipedia, Methods of computing square-roots, Section 12, accessed September 2018 at https://en.wikipedia.org/wiki/Methods_of_computing_square_rootsGoogle Scholar
2. Wikipedia, Pell's equation, Section 4, accessed September 2018 at https://en.wikipedia.org/wiki/Pell's_equationGoogle Scholar
3. Olds, C. D., Continued fractions. Random House (1963), available at http://www.ms.uky.edu/∼sohum/ma330/files/Continued%20Fractions.pdfGoogle Scholar
4. O'Connor, J. J. and Robertson, E. F., Pell's equation, accessed September 2018 at http://www-groups.dcs.st-and.ac.uk/history/HistTopics/Pell.htmlGoogle Scholar
5. Surendran, K., Babu, D. K., Gendler, S. and Bhattacharya, D., The house number puzzle: solution through bifurcation, πME Journal 14 (2017) pp. 389-397.Google Scholar
6. Sloane, N. J. A. (founder), The online encyclopaedia of integer sequences, accessed September 2018 at https://oeis.org/Google Scholar

