Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-13T10:27:37.112Z Has data issue: false hasContentIssue false
  • English
  • Français

The factorial function: convex functions, the Bohr-Mollerup-Artin theorem, and some formulae

Published online by Cambridge University Press:  01 August 2016

David Fowler
David Fowler*
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL
Get access Rights & Permissions [Opens in a new window]

Extract

How might we define x!? This is the next in my series of articles [1-3]; by now we know quite a bit about the factorial function, except that we have no real definition of it, nothing that would allow us to evaluate, say, ½!. So how do we move on to the next stage?

There is a range of strategies. We could find or manufacture a suitable function f that satisfies the basic relations

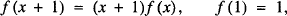
and adopt it as our definition.

Type
Articles
Information
The Mathematical Gazette , Volume 84 , Issue 501 , November 2000 , pp. 433 - 441
Copyright
Copyright © The Mathematical Association 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Fowler, D. H. A simple approach to the factorial function, Math. Gaz. 80 (July 1996) pp. 378–381.Google Scholar
2. Fowler, D. H. A simple approach to the factorial function – the next step, Math. Gaz. 83 (March 1999) pp. 53–57.Google Scholar
3. Fowler, D. H. The factorial function: Stirling’s formula, Math. Gaz. 84 (March 2000) pp. 42–50.Google Scholar
4. Artin, E. The Gamma Function, Holt, Rienhart and Winston, New York (1964), a translation by Butler, M. of ‘Einführung in die Theorie der Gammafunktion’, Hamburger Mathematische Einzelschriften 1, Teubner, Leipzig (1931).Google Scholar
5. Bourbaki, N. Éléments de mathématiques, Chapitre VII, ‘La fonction gamma’, of Première Partie, Livre IV, ‘Fonctions d’une variable réelle’, Gautier Villars, Paris.Google Scholar
6. Whittaker, E. T. and Watson, G. N. A course of modem analysis, Cambridge University Press (1902 and often revised and reprinted).Google Scholar