Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-11T00:21:21.626Z Has data issue: false hasContentIssue false
  • English
  • Français

Fibonacci-Lucas hyperbolas

Published online by Cambridge University Press:  22 June 2022

Howard Sporn
Howard Sporn*
Affiliation:
Department of Mathematics and Computer Science, Queensborough Community College, Bayside, NY, USA 11364 e-mail: hsporn@qcc.cuny.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Let us define a Fibonacci-Lucas hyperbola as a hyperbola passing through an infinite number of points of the form (Fm, Ln), where the Fm are distinct Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21,…, where F0 = 0), and the Ln are distinct Lucas numbers (2, 1, 3, 4, 7, 11, 18, 29,…,. where L0 = 2). The simplest examples are 5x2 - y2 = 4, which contains the points (Fk, Lk) with odd subscripts, e.g. (1, 1), (2, 4), (5, 11), and 5x2 - y2 = -4, which contains the points with even subscripts, e.g. (0, 2), (1, 3), (3, 7); (see [1, 2]). These follow immediately from the identity (1)

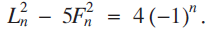$$L_n^2 - 5F_n^2 = 4{( - 1)^n}.$$
Our goal is to find more of these Fibonacci-Lucas hyperbolas.

Type
Articles
Information
The Mathematical Gazette , Volume 106 , Issue 566 , July 2022 , pp. 242 - 246
Check for updates
Copyright
© The Authors, 2022 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Georghiou, C. and Brady, W. G., Fibonacci-Lucas hyperbola for odd n, in elementary problems and solutions, Fibonacci Quarterly, 25 (1987), p. 181.Google Scholar
Lee, J. Z., Lee, J. S., and Brady, W. G., Fibonacci-Lucas hyperbola for even n, in elementary problems and solutions, Fibonacci Quarterly, 25 (1987), p. 181.Google Scholar
Kimberling, C., Fibonacci hyperbolas, Fibonacci Quarterly, 28 (1990), pp. 22–27.Google Scholar
Koshy, T., Fibonacci and Lucas Numbers with applications, Wiley (2001).Google Scholar