Article contents
A footnote to the theory of double integrals
Published online by Cambridge University Press: 23 January 2015
Extract
The probability integral theorem, which states that

is on the record for having enticed numerous mathematicians to find alternative proofs for it, over a period of more than two centuries, till recent times (for a few recent references see [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]). The most popular demonstration (attributed to the French mathematician Poisson; see [11], in references of [12]), the one found in almost all textbooks, relies on the double integral
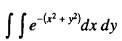
(taken over the upper-right quarter of the Cartesian plane) obtained by squaring the probability integral. By resorting to polar coordinates and writing down the above integral as:
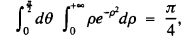
the value of the probability integral is obtained by taking the square root of the result on the right-hand side of this latter relation.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2010
References
- 1
- Cited by

