Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T07:37:44.902Z Has data issue: false hasContentIssue false
  • English
  • Français

A graph related to the Euler ø function

Published online by Cambridge University Press:  03 July 2023

Nima Ghanbari  and
Saeid Alikhani
Nima Ghanbari
Affiliation:
Department of Informatics University of Bergen P.O. Box 7803, 5020 Bergen, Norway e-mail: Nima.Ghanbari@uib.no
Saeid Alikhani
Affiliation:
Department of Mathematics, Yazd University. 89195-741, Yazd, Iran e-mail: alikhani@yazd.ac.ir
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph G is a pair G = (V, E), where V and E are the vertex set and the edge set of G, respectively. The order and size of G is the number of vertices and edges of G, respectively. The degree or valency of a vertex u in a graph G (loopless), denoted by deg (u), is the number of edges meeting at u. If, for every vertex ν in G, deg (ν) = k, we say that G is a k-regular graph. The cycle of order n is denoted by Cn and is a connected 2-regular graph. The path graph of order n is denoted by Pn and obtain by deleting an edge of Cn. A tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected undirected graph without cycle. A leaf (or pendant vertex) of a tree is a vertex of the tree of degree 1. An edge of a graph is said to be pendant if one of its vertices is a pendant vertex. A complete bipartite graph is a graph G with 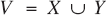and 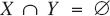such that every vertex of the set (part) X is connected to every vertex of the set (part) Y. If , then this graph is denoted by Km,n. The complete bipartite graph K1,n is called the star graph which has n + 1 vertices. The distance between two vertices u and ν of G, denoted by d (u, ν), is defined as the minimum number of edges of the walks between them. The complement of graph G is denoted by 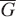and is a graph with the same vertices such that two distinct vertices of 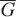are adjacent if, and only if, they are not adjacent in G. For more information on graphs, refer to [1].

Type
Articles
Information
The Mathematical Gazette , Volume 107 , Issue 569 , July 2023 , pp. 263 - 272
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Authors, 2023. Published by Cambridge University Press on behalf of The Mathematical Association

References

Bondy, J. A. and Murty, U. S. R., Graph theory with applications, Elsevier (1976).CrossRefGoogle Scholar
Pillai, S. Sivasankaranarayana, On a function connected with ø(n), Bull. Amer. Math. Soc. 35 (1929) pp. 837–841.CrossRefGoogle Scholar
Loomis, P., Plytage, M., and Polhill, J., Summing up the Euler ø function, The College Math. J. 39(1) (2008) pp. 34–42.CrossRefGoogle Scholar
Frucht, R. and Harary, F., On the corona of two graphs, Aequationes Math. 4 (1970) pp. 322–324.CrossRefGoogle Scholar
Alikhani, S. and Iranmanesh, M.A., Hosoya polynomial of dendrimer nanostar D 3 [n], MATCH Commun. Math. Comput. Chem. 71 (2014) pp. 395–405.Google Scholar
Deutsch, E. and Klavzar, S., Computing the Hosoya polynomial of graphs from primary subgraphs, MATCH Commun. Math. Comput. Chem. 70 (2013) pp. 627–644.Google Scholar
Rashid, M. A., Ahmad, S., Cancan, M. and Muhammad, M. H., Topological properties of nanostar dendrimer and smart polymer, J. Chem. 2020, Article ID 1280632, also available at ad560c586336e682e7585af0571bd793c2bf.pdfGoogle Scholar