Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-25T00:59:56.820Z Has data issue: false hasContentIssue false
  • English
  • Français

How many real attractive fixed points can a polynomial have?

Published online by Cambridge University Press:  14 February 2019

Terence Coelho  and
Bahman Kalantari
Terence Coelho
Affiliation:
Mathematics Department, Rutgers University, USA e-mail: terencejcoelho96@gmail.com
Bahman Kalantari
Affiliation:
Department of Computer Science, Rutgers University, USA e-mail: kalantari@cs.rutgers.edu
Get access Rights & Permissions [Opens in a new window]

Extract

While the notion of roots of a quadratic polynomial is rudimentary in high school mathematics, that of its fixed points is uncommon. A real or complex number is a fixed point of a polynomial p (x) p (θ) = θ. The fact that the notion of fixed point of polynomials is not commonly covered in high school or undergraduate mathematics is surprising because the relevance of the fixed points of a quadratic can be demonstrated easily via iterative methods for the approximation of such numbers as 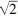, when the quadratic formula offers no remedy.

Type
Articles
Information
The Mathematical Gazette , Volume 103 , Issue 556 , March 2019 , pp. 65 - 76
Copyright
Copyright © Mathematical Association 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Devaney, R. L., A first course in chaotic dynamic system theory and experiment (ABP) (1992).Google Scholar
2. Mandelbrot, B. B., Fractal geometry of nature, W. F. Freeman, New York (1993).10.21236/ADA273271Google Scholar
3. Kalantari, B., Polynomial root-finding and polynomiography, World Scientific, Hackensack, NJ (2008).10.1142/6265Google Scholar
4. Beardon, A. F., Iteration of rational functions: Complex analytic dynamical systems, Springer-Verlag, NY (1991).10.1007/978-1-4612-4422-6Google Scholar
5. Milnor, J., Dynamics in one complex variable: Introductory lectures, Vol 160 (3rd edn.) Princeton University Press, NJ (2006).Google Scholar
6. Burden, R. L., Faires, J. D., Numerical Analysis, Brooks Cole, Pasicif Grove, CA (2004).Google Scholar