Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gordon, Russell A.
2025.
Evaluating Some Improper Sine and Cosine Integrals.
Axioms,
Vol. 14,
Issue. 11,
p.
811.

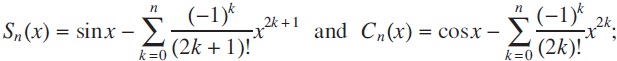
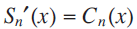 for each
for each  and
and 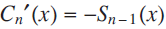 for each
for each 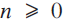 . It is known that
. It is known that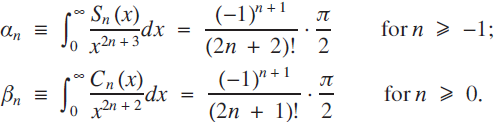
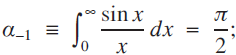
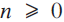 then follow rather easily using induction and integration by parts. (Details are provided in the Appendix.)
then follow rather easily using induction and integration by parts. (Details are provided in the Appendix.)
