Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T07:44:06.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Irrationality proofs à la Hermite

Published online by Cambridge University Press:  23 January 2015

Li Zhou
Li Zhou*
Affiliation:
Department of Mathematics, Polk State College, Winter Haven, FL 33881, USA e-mail:, lzhou@polk.edu
Get access Rights & Permissions [Opens in a new window]

Extract

In [1] Niven used the integral

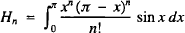
to give a well-known proof of the irrationality of π. Recently Zhou and Markov [2] used a recurrence relation satisfied by this integral to present an alternative proof which may be more direct than Niven's.

Niven did not cite any references in [1] and thus the origin or Hn seems rather mysterious and ingenious. However if we heed Abel's advice to ‘study the masters’, we find that Hn emerged much more naturally from the great works of Lambert [3] and Hermite [4].

Type
Articles
Information
The Mathematical Gazette , Volume 95 , Issue 534 , November 2011 , pp. 407 - 413
Copyright
Copyright © The Mathematical Association 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Niven, I., A simple proof that π is irrational, Bull. Amer. Math. Soc. 53 (1947) 509; available at http://www.ams.org/journals/bull/1947-53-06/.Google Scholar
2. Zhou, L. and Markov, L., Recurrent proofs of the irrationality of certain trigonometric values, Amer. Math. Monthly 117 (2010) pp. 360–362.Google Scholar
3. Lambert, J. H., Mémoires sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques, Mém. de l'Acad. R. des Sci. de Berlin 17 (1761/1768) pp. 265–322; available at http://www.kuttaka.org/~JHL/L1768b.html.Google Scholar
4. Hermite, C., Sur l'expression U sin x + V cos x + W , J. de Crelle 76 (1873) pp. 303–312; Sur quelques approximations algébriques, J. de Crelle 76 (1873) pp. 342-344; also in Oeuvres de Charles Hermite, vol. III, Gauthier-Villars, Paris, 1912; available at http://www.math.uni-bielefeld.de/~rehmann/DML/dml_links_author_H.html.Google Scholar
5. Polyanin, A. D., Laplace transforms: Expressions with trigonometric functions, available at http://eqworld.ipmnet.rulen/auxiliary/inttrans/laplace6.pdf.Google Scholar
6. Boros, G. and Moll, V. H., Irresistible integrals, Cambridge University Press (2004).Google Scholar
7. Whittaker, E. T. and Watson, G. N., A course of modem analysis (4th edn.), Cambridge University Press (2002).Google Scholar