Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Misra, Vandana
Choudhury, P. K.
Khastgir, P.
and
Ojha, S. P.
1996.
Electromagnetic wave propagation through a dielectric guide having Piet Hein cross-sectional geometry.
Microwave and Optical Technology Letters,
Vol. 12,
Issue. 5,
p.
250.
Gielis, Johan
Beirinckx, Bert
and
Bastiaens, Edwin
2003.
Superquadrics with rational and irrational symmetry.
p.
262.
Gielis, Johan
2003.
A generic geometric transformation that unifies a wide range of natural and abstract shapes.
American Journal of Botany,
Vol. 90,
Issue. 3,
p.
333.
Seaby, A W
Thomas, M
and
Ryde, S J S
2004.
Implementation of a spreadsheet program for calculation of equivalent square field size.
The British Journal of Radiology,
Vol. 77,
Issue. 920,
p.
672.
Zaharia, Sorin
and
Birn, J.
2007.
Adiabatic plasma equilibrium and application to a reconnection problem.
Physics of Plasmas,
Vol. 14,
Issue. 7,
Yajima, T.
and
Nagahama, H.
2007.
Kawaguchi space, Zermelo's condition and seismic ray path.
Nonlinear Analysis: Real World Applications,
Vol. 8,
Issue. 1,
p.
130.
Bera, N.
Bhattacharjee, J. K.
Mitra, S.
and
Khastgir, S. P.
2008.
Energy levels of a particle confined in a super-circular box.
The European Physical Journal D,
Vol. 46,
Issue. 1,
p.
41.
Richardson, Jane S.
Schneider, Bohdan
Murray, Laura W.
Kapral, Gary J.
Immormino, Robert M.
Headd, Jeffrey J.
Richardson, David C.
Ham, Daniela
Hershkovits, Eli
Williams, Loren Dean
Keating, Kevin S.
Pyle, Anna Marie
Micallef, David
Westbrook, John
and
Berman, Helen M.
2008.
RNA backbone: Consensus all-angle conformers and modular string nomenclature (an RNA Ontology Consortium contribution).
RNA,
Vol. 14,
Issue. 3,
p.
465.
Chakraborty, S
Bhattacharjee, J K
and
Khastgir, S P
2009.
An eigenvalue problem in two dimensions for an irregular boundary.
Journal of Physics A: Mathematical and Theoretical,
Vol. 42,
Issue. 19,
p.
195301.
Panda, S.
Chakraborty, S.
and
Khastgir, S. P.
2011.
Eigenvalue problem in two dimensions for an irregular boundary: Neumann condition.
The European Physical Journal Plus,
Vol. 126,
Issue. 7,
Sadowski, A.J.
2011.
Geometric properties for the design of unusual member cross-sections in bending.
Engineering Structures,
Vol. 33,
Issue. 5,
p.
1850.
Forestiere, Carlo
Iadarola, Giovanni
Dal Negro, Luca
and
Miano, Giovanni
2011.
Near-field calculation based on the T-matrix method with discrete sources.
Journal of Quantitative Spectroscopy and Radiative Transfer,
Vol. 112,
Issue. 14,
p.
2384.
Mahmood, Ansar
Wang, Xin Wei
and
Zhou, Chu Wei
2011.
Generic Geometric Model for 3D Woven Interlock Composites.
Advanced Materials Research,
Vol. 399-401,
Issue. ,
p.
478.
Panda, Subhasis
Guha Sarkar, Tapomoy
and
Khastgir, Sugata Pratik
2012.
Metric Deformation and Boundary Value Problems in 2D.
Progress of Theoretical Physics,
Vol. 127,
Issue. 1,
p.
57.
Sadowski, Adam J.
and
Michael Rotter, J.
2013.
Exploration of novel geometric imperfection forms in buckling failures of thin-walled metal silos under eccentric discharge.
International Journal of Solids and Structures,
Vol. 50,
Issue. 5,
p.
781.
Martinelli, Francesco
Possieri, Corrado
and
Tornambe, Antonio
2014.
Motion planning for a unicycle-like mobile robot, using algebraic attractive curves.
p.
1335.
Panda, S.
and
Hazra, G.
2014.
Boundary perturbations and the Helmholtz equation in three dimensions.
The European Physical Journal Plus,
Vol. 129,
Issue. 4,
Matsuura, Masaya
2015.
Gielis’ superformula and regular polygons.
Journal of Geometry,
Vol. 106,
Issue. 2,
p.
383.
Li, Shan
and
Boyd, John P.
2015.
Approximation on non-tensor domains including squircles, Part III: Polynomial hyperinterpolation and radial basis function interpolation on Chebyshev-like grids and truncated uniform grids.
Journal of Computational Physics,
Vol. 281,
Issue. ,
p.
653.
Li, Shan
and
Boyd, John P.
2015.
Spectral methods in non-tensor geometry, Part II: Chebyshev versus Zernike polynomials, gridding strategies and spectral extension on squircle-bounded and perturbed-quadrifolium domains.
Applied Mathematics and Computation,
Vol. 269,
Issue. ,
p.
759.

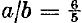 and
and 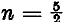 . Derivatively, Gerald Robinson, a Toronto architect, has incorporated a superelliptic parking garage into a shopping complex (called a Superblock) in downtown Peterborough, Ontario; the parameters are
. Derivatively, Gerald Robinson, a Toronto architect, has incorporated a superelliptic parking garage into a shopping complex (called a Superblock) in downtown Peterborough, Ontario; the parameters are 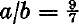 and n = 2.71828 … (the exponential coefficient). In such urban contexts the two-parameter super-ellipse is efficiently tailorable to the dimensions of the site. It is said to be very elegant.
and n = 2.71828 … (the exponential coefficient). In such urban contexts the two-parameter super-ellipse is efficiently tailorable to the dimensions of the site. It is said to be very elegant.
