No CrossRef data available.
Article contents
Linear differential equations with constant coefficients
Published online by Cambridge University Press: 06 June 2019
Extract
We consider the second order homogeneous linear differential equation(H)$${ ay'' + by' + cy = 0 }$$with real coefficients a, b, c, and a ≠ 0. The function y = emx is a solution if, and only if, m satisfies the auxiliary equation am2 + bm + c = 0. When the roots of this are the complex conjugates m = p ± iq, then y = e(p ± iq)x are complex solutions of (H). Nevertheless, real solutions are given by y = c1epx cos qx + c2epx sin qx.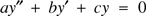
Information
- Type
- Articles
- Information
- Copyright
- © Mathematical Association 2019
References
Plumpton, C. and Tomkys, W. A.: Sixth form pure mathematics, Volume two, Pergamon Press (1963).Google Scholar

