Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T07:40:25.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Lobb's generalisation of Catalan's parenthesisation problem revisited

Published online by Cambridge University Press:  23 January 2015

Thomas Koshy
Thomas Koshy*
Affiliation:
Department of Mathematics, Framingham State University, Framingham, MA 01701-9101, USA
Get access Rights & Permissions [Opens in a new window]

Extract

In 1838, the Belgian mathematician Eugene C. Catalan (1814-1894) discovered that the number Cn of well-fonned sequences, with n pairs of left and right parentheses, is given by 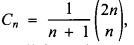where n > 0 [1, 2]. For example, there are exactly five well-formed sequences with three pairs of left and right parentheses: ()()(), ()(()), (())(), (()()), ((())). The case n = 0 yields the null sequence, often denoted by λ. Notice that ()) and ((()()), for example, are not correctly parenthesised.

Type
Articles
Information
The Mathematical Gazette , Volume 96 , Issue 535 , March 2012 , pp. 56 - 65
Copyright
Copyright © The Mathematical Association 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Cohen, D. I. A., Basic techniques of combinatorial theory, Wiley, New York (1978).Google Scholar
2. Koshy, T., Catalan numbers with applications, Oxford University Press, New York (2009).Google Scholar
3. Larcombe, P. J., The 18th century Chinese discovery of the Catalan numbers, Mathematical Spectrum 32 (1999) pp. 5–7.Google Scholar
4. Clarke, R. J., Letter to the Editor, Mathematics Magazine 61 (1988), p.269.Google Scholar
5. Stanley, R. P., Enumerative combinatorics, Vol. 2, Cambridge University Press, New York (1999).CrossRefGoogle Scholar
6. Koshy, T., Lobb's generalization of Catalan's parenthesization problem, College Mathematics Journal 40 (2009) pp. 99–107.CrossRefGoogle Scholar
7. Lobb, A., Deriving the nth Catalan number, Math. Gaz. 83 (March 1999) pp. 109–110.CrossRefGoogle Scholar
8. Shapiro, L. W., A Catalan triangle, Discrete Mathematics 14 (1976), pp. 83–90.CrossRefGoogle Scholar
9. Koshy, T., Elementary number theory with applications (2nd edn.), Academic Press, Burlington, MA (2007).Google Scholar
10. Koshy, T. and Salmassi, M., Parity and primality of Catalan numbers, College Mathematics Journal 37 (2006) pp. 52–53.CrossRefGoogle Scholar
11. Shapiro, L. W., Problem 10753, American Mathematical Monthly 106 (1999) p. 777.CrossRefGoogle Scholar
12. DiDomenico, A. S., Private communications, 2008.Google Scholar
13. Graham, R. L. et a1, Concrete mathematics, Addison-Wesley, Reading, MA (1990).Google Scholar
14. Beiler, A. H., Recreations in the theory of numbers (2nd edn.), Dover, New York (1966).Google Scholar