No CrossRef data available.
Article contents
A lower bound for the prime counting function
Published online by Cambridge University Press: 23 January 2015
Extract
Let π (x) count the primes p ≤ x, where x is a large real number. Euclid proved that there are infinitely many primes, so that π (x) → ∞ as x → ∞; in fact his famous argument ([1: Section 2.2]) can be used to show that
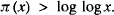
There was no further progress on the problem of the distribution of primes until Euler developed various tools for the purpose; in particular he proved in 1737 [1: Theorem 427] that
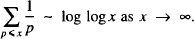
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2011
References
1.
Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers (4th edn.), Oxford University Press (1960).Google Scholar

