Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-25T01:24:26.657Z Has data issue: false hasContentIssue false
  • English
  • Français

Metric relations in crossed trapezia

Published online by Cambridge University Press:  18 June 2018

Martin Josefsson
Martin Josefsson*
Affiliation:
Västergatan 25d, 285 37 Markaryd, Sweden e-mail: martin.markaryd@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Extract

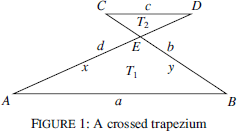
The trapezium (trapezoid in American English) is one of the seven most well-known quadrilaterals that is studied in school geometry. However, it is always assumed that it is convex. In this note we shall derive metric formulas for the most important quantities in crossed trapezia and compare them to the similar formulas for convex trapezia. The corresponding investigation regarding crossed cyclic quadrilaterals was conducted in [1]. Any crossed quadrilateral has a pair of opposite sides intersecting and both of its diagonals are outside of itself.

Type
Articles
Information
The Mathematical Gazette , Volume 102 , Issue 554 , July 2018 , pp. 264 - 269
Copyright
Copyright © Mathematical Association 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Josefsson, M., Metric relations in crossed cyclic quadrilaterals, Math. Gaz. 101 (November 2017) pp. 499–502.CrossRefGoogle Scholar
2. Coxeter, H. S. M. and Greitzer, S. L., Geometry revisited, Math. Ass. Amer. (1967).CrossRefGoogle Scholar
3. de Villiers, M., Slaying a geometrical monster: Finding the area of a crossed quadrilateral, Learning and Teaching Mathematics 18 (June 2015) pp. 23–28. Also available at http://dynamicmathematicslearning.com/crossed-quad-area.pdfGoogle Scholar
4. Wolfram MathWorld, Trapezoid, accessed January 2018, http://mathworld.wolfram.com/Trapezoid.htmlGoogle Scholar
5. Josefsson, M., Characterizations of trapezoids, Forum Geom. 13 (2013) pp. 23–35.Google Scholar