No CrossRef data available.
Article contents
A new algorithm for computing the logarithmic function
Published online by Cambridge University Press: 01 August 2016
Extract
The values of many functions, for example sinx or cosx, can be computed efficiently for arbitrary values of x from their known power series expansions. However, for the logarithmic function this is not so straightforward. There does not exist an expansion of ln x as a power series in x, the closest to it mathematically being an infinite power series in 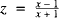 of the form
of the form
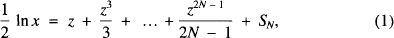
where 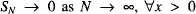 (see [1]).
(see [1]).
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2005
References
1.
Abramowitz, M. and Stegun, I. A.
Handbook of mathematical functions, Dover Publications (1965) p. 68.Google Scholar
2.
Press, W. H.
Flannery, B. P.
Teukolsky, S. A. and Vetterling, W. T.
Numerical recipes – the art of scientific computing, Cambridge University Press (1987).Google Scholar

