No CrossRef data available.
Article contents
New points from old
Published online by Cambridge University Press: 23 January 2015
Extract
Given two rational points on the graph of a cubic polynomial with rational coefficients, it is well known that one can construct another rational point by finding the third intersection point of the curve with the chord through the two points. For example, consider the two points A (2, 15) and B(0, 3) on y = 2x3 − x2 + 3.
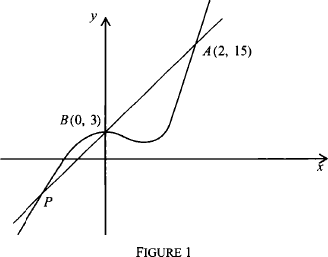
The chord through A and B has equation y = 6x + 3 and this intersects the curve again at the point P, where
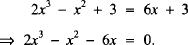
This cubic equation has three roots corresponding to A, B and the new point P,
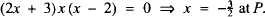
P is the point 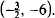
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2012

