Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T07:09:32.970Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Associate Powers and a Functional Equation

Published online by Cambridge University Press:  03 November 2016

I. M. H. Etherington
Get access Rights & Permissions [Opens in a new window]

Extract

Several writers have studied algebras in which multiplication is non-associative, that is, x yz≠xy z. It is necessary in a non-associative algebra to distinguish the possible interpretations of a power xn In a non-commutative non-associative algebra x2 is unique, x3 can mean xx2 or x2x; x4 can mean x xx2, x x2x, x2x2, xx2x or x2x x, x5 has 14 interpretations; x6 has 42; and so on. In a commutative non-associative algebra, the possible interpretations are fewer x3 is unique, x4 can mean xx3 or x2x2, x5 can mean x xx3, x x2x2 or x2x3, x6 has 6 interpretations, and so on. The problem considered here is how many meanings are there for xn (A) in a general non-commutative non-associative algebra ? (B) in a general commutative non-associative algebra ? The answer to (A) is 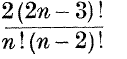I am not able to find any such simple formula for (B).

Type
Research Article
Information
The Mathematical Gazette , Volume 21 , Issue 242 , February 1937 , pp. 36 - 39
Copyright
Copyright © Mathematical Association 1937

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page no 36 note * E.g. De Morgan, , Trans. Camb. Phil Soc., 8 (1844), 241 Google Scholar; Dickson, , Trans. Amer. Math. Soc., 13 (1912), 60 CrossRefGoogle Scholar. Jordan, Göttingen Nachr., 1932, 569; 1933, 209, deals with an application to Quantum Mechanics. A forthcoming paper by the author on Genetics uses commutative non-associative algebras.

page no 36 note † Though not in the algebras considered by Jordan.