No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 25 August 2015
In this note we define and study certain subsets of the solutions of the Diophantine equations of the type
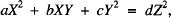(1)
the coefficients a, b, c and d being integers, with gcd(a, b, c) = 1, and values of the unknowns X, Y and Z sought in rational numbers or integers, with X, Y, Z not all zero. Since (1) is a homogeneous equation it is elementary to pass from rational solutions to integral ones, and also in reverse. We chose to work with rational numbers because of the flexibility in computation they allow. This flexibility will enable us to prove that, under certain conditions, with three distinct solutions we can build infinite subsets of new solutions of (1), the properties of which are the main topic of this note.
As documented by L. E. Dickson [1], formulae said to give all the solutions, either of this general equation (1) or some particular cases, have appeared in the literature at least since the first half of the 17th century. Dickson himself provided the general formulae expressing all the solutions of (1) in rational numbers from an already found particular solution [2, pp. 44-45]. Similar study and formulae are part of a recent article [3, Lemma 2-1] where the solutions of (1) are applied to the study of a particular lattice. In essence these formulae prove that from any single solution of (1) we can compute all the others, which form an infinite set.