No CrossRef data available.
Article contents
On the Approximation to Irrational Numbers By Rationals
Published online by Cambridge University Press: 03 November 2016
Extract
The problem of deciding whether a given number is irrational or not is frequently one of some difficulty, as in the proof that π is irrational. Several numbers which are very probably irrational have never been proved so, e.g. y, eπ . However, we have one quite simple test for deciding whether a number is irrational or not when we have the number expressed as a continued fraction, viz. if the continued fraction terminates, the number is rational; if not, irrational. In what follows we assume our irrational number given as a continued fraction :
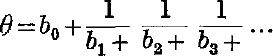
or shortly
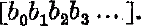
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1927
References
Page 363 note * Heawood; I.e. infra, ser. 2, vol. 20, p. 233.

