Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T03:29:05.513Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Necessity of Placing the Sign × before the Multiplicand

Published online by Cambridge University Press:  03 November 2016

Saradakanta Ganguli
Saradakanta Ganguli*
Affiliation:
Ravenshaw College, Cuttack, India
Get access Rights & Permissions [Opens in a new window]

Extract

Among many English writers of text-books on arithmetic and algebra there appears to exist a state of confusion regarding the use of the sign of multiplication. Here are three instances. Godfrey and Price’s Arithmetic (1915) contains the following statement:

“The sign × means multiplied by; thus 3 ft. × 7 = 21 ft., and (7 × 3) ft. = 21 ft.; but 7 × 3 ft. is unmeaning ” (p. 13). Yet, on page 147, we find the expressions

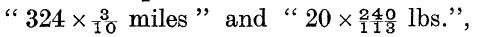
in which multipliers precede the corresponding multiplicands.

Type
Research Article
Information
The Mathematical Gazette , Volume 16 , Issue 221 , December 1932 , pp. 320 - 323
Copyright
Copyright © Mathematical Association 1932

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page no 320 note * But Workman would read 34 × 6 as thirty-four times six.

page no 320 note † Wood’s Algebra, revised by Lund (13th edition, 1848), p. 30, seems to contain Wood’s view on the subject.

page no 320 note ‡ Hind’s Algebra (5th edition, 1841), p. 4.

page no 320 note § Peacock’s Algebra, vol. i. (1842), p. 5.

page no 320 note ‖ De Morgan’s Elements of Arithmetic (1857), p. 26, Art. 53; but he also places the multiplier before the multiplicand in the statement “£2=2 × £1” (p. 139).

page no 320 note ¶ Chrystal’s Algebra, vol. i. (2nd edition, 1889), p. 11.

page no 320 note $ A Treatise on Arithmetic (4th edition, 1877), p. 17 But on page 128 the multiplier is written after the multiplicand in some cases.

page no 320 note ** Wood’s Algebra, remodelled by Lund (18th edition, 1878), p. 2.

page no 320 note †† Elements of Algebra, translated into English by Hewlett (4th edition, 1828), pp. 6 and 7.

page no 321 note * Chrystal’s Algebra, vol. i. (1889), p. 4.

page no 321 note † Chrystal’s Algebra, vol. i. p. 11.

page no 322 note * A History of Mathematical Notations, vol. i. (1928), p. 265, Art. 231.

page no 322 note † Ibid. p. 252. These ways have been enumerated by Cajori as follows: “(1) in solutions of problems by the process of two false positions, (2) in solving problems in compound proportion involving integers, (3) in solving problems in simple proportion involving fractions, (4) in the addition and subtraction of fractions, (5) in the division of fractions, (6) in checking results of computation by the processes of casting out the 9’s, 7’s, or ll’s, (7) as part of a group of lines drawn as guides in the multiplication of one integer by another, (8) in reducing radicals of different orders to radicals of the same order, (9) in computing on lines, to mark the line indicating ‘thousands’, (10) to take the place of the multiplication table above 5 times 5, and (11) in dealing with amicable numbers”.

page no 322 note ‡ Cajori, , A History of Mathematical Notations, vol. i. p. 270 Google Scholar.

page no 323 note * De Morgan, Elements of Arithmetic, p. 19.