Article contents
Operational Methods in Mathematical Physics
Published online by Cambridge University Press: 03 November 2016
Extract
1. The reviewer of Berg’s Operational Calculus as applied to Engineering and Physics (2nd ed. 1936) in the Gazette (Oct. 1937, p. 309) remarks that “Heaviside’s methods deserve more attention in this country than they appear to receive”, and a reference is made to articles contributed by Bromwich, Jeffreys and myself to Vol. XIV in 1928.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1938
References
Page No 264 Note * Phil Mag., (7) 7 (1929), 1153.
Page No 265 Note * Since his first paper, “Über das Problem der Wärmeleitung”, Jahresbericht d. deutsch. Math. Vereinigung, 33 (1925), Doetsch has in many papers advocated the use of the Laplace Transformation in such questions, and his important book, Theorie u. Anwendung der Laplace-Transformation, (Berlin), has appeared in 1938. His work thus anticipated van der Pol’s, which depends on the same principle.
But, since writing this paper, I have learnt that Bateman, in the Proc. Gamb. Phil. Society, 15 (1910), 423, anticipated both. See also Bateman’s Partial Differential Equations of Mathematical Physics (1932), p. 46.
Page No 265 Note † There is a short paper by Itoo, T., in the Tôkohu Math. Journal, 42 (1936) entitled “Pseudo-operational Calculus”, the idea being much the same as in this article.
Page No 266 Note * It is known that, when 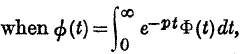 , there cannot be more than one continuous function Φ(t) satisfying this relation.
Cf.Lerch, , Acta Math., 27 (1903), 339
CrossRefGoogle Scholar.
, there cannot be more than one continuous function Φ(t) satisfying this relation.
Cf.Lerch, , Acta Math., 27 (1903), 339
CrossRefGoogle Scholar.
Page No 269 Note * Compare the solution of these equations given in Bromwich’s paper, Proc. London Math. Soc. (2), 15 (1916), 409.
Page No 271 Note * This theorem is sometimes said to be derived from Fourier’s Integral, but the “proof” is purely formal.
E.g. by Fourier”s Integral we have
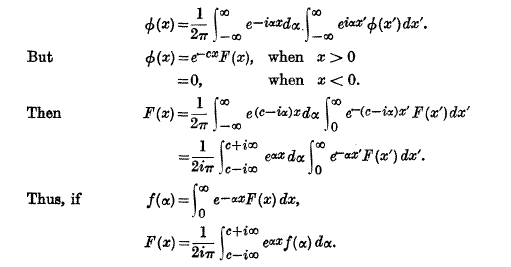
A Simple proof, stating conditions imposed upon f(p), given by Churchill in Math. Zeitschrift, 42(1937), 569.
Page No 272 Note * This involves a further assumption as to the nature of v.
Page No 273 Note * This well-known integral can be obtained from
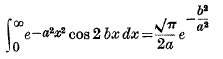
by integrating with respect to b from 0 to b.
Page No 276 Note * Since the integrand is a single-valued function of λ.
Page No 278 Note * Cf. Watson, Beseel Functions, p. 78.
Page No 279 Note * Cf. Jeffrey’s Tract on Operational Methods (2nd ed.), p. 51.
Page No 280 Note * It has been noticed in § 10 that some additional conditions have been imposed on v. This seems unavoidable. See Titchmarsh, Fourier Integrals (1937), 10.6-10.14.
- 6
- Cited by


