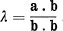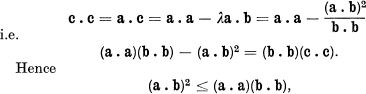Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1978.
Journal of the Japan Society of Colour Material,
Vol. 51,
Issue. 10,
p.
606.
Zuo, Lin
Bai, Lan
and
Wang, Zhen
2024.
Unsupervised Evaluation Metrics for Plane-based Clustering.
p.
5631.