Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grattan-Guinness, I.
2013.
On proving certain optimisation theorems in plane geometry.
The Mathematical Gazette,
Vol. 97,
Issue. 538,
p.
75.

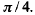 between a diagonal and the longer attached side. Circumscribe around R any other rectangle M that carries the corners of R on its sides, and let its proportion angle be
between a diagonal and the longer attached side. Circumscribe around R any other rectangle M that carries the corners of R on its sides, and let its proportion angle be 