Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T06:45:32.931Z Has data issue: false hasContentIssue false
  • English
  • Français

Reciprocally related primes

Published online by Cambridge University Press:  12 November 2024

Damjan Kobal
Damjan Kobal*
Affiliation:
Department of Mathematics Faculty of Mathematics and Physics, University of Ljubljana Jadranska 19, 1000 Ljubljana, Slovenia e-mail: damjan.kobal@fmf.uni-lj.si
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Number theory and especially primes are an infinite source of inspirational ideas in elementary mathematics. Many of these ideas can be understood and some also explained with very basic mathematical knowledge. In our paper we explain the cycle which appears between the first six multiples of the decimal expression of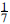 and explore an inspiringly simple relation between primes, which somehow makes them gather into mysterious groups. And while exploring these simple questions, we are led to unveil some aspects of the power and limits of human mind and those of a computer.

Type
Articles
Information
The Mathematical Gazette , Volume 108 , Issue 573 , November 2024 , pp. 450 - 459
Check for updates
Copyright
© The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association

References

Tattersall, J. J., Elementary number theory in nine chapters (2nd edn.) Cambridge (2005).CrossRefGoogle Scholar
RSA numbers, Wikipedia, accessed April 2024 at https://en.wikipedia.org/wiki/RSAnumbers Google Scholar
The Cunningham Project, accessed April 2024 at https://homes.cerias.purdue.edu/∼ssw/cun/ Google Scholar
Kobal, Damjan, Factorisation of 101540 – 1, accessed March 2024 at https://ko.fmf.uni-lj.si/fact/Factor-10-to-1540-1.pdf Google Scholar