Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:41:35.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Regular polygons on sides of special triangles

Published online by Cambridge University Press:  01 August 2016

Zvonko Čerin
Zvonko Čerin*
Affiliation:
Kopernikova 7, 10010 Zagreb, Croatia, e-mail: CERIN@MATH.HR
Get access Rights & Permissions [Opens in a new window]

Extract

For a natural number n ≥ 3 and a positive real number ξ let Pn (ξ) denote the area of the regular n-gon with side of length ξ and let P(ABC … Z) be the area of a convex polygon ABC … Z.

In 1996 Josip Kovačević observed [1] that in every triangle ABC with sides a, b and c and with the angle A equal to π/3 radians the following relation holds:

Similarly, if the angle A is equal to 2π/3 radians then

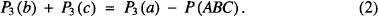
On the other hand, when the angle A is π/2 radians, then Pythagoras’ theorem implies 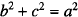which could be rewritten as so

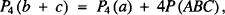
because P(ABC) = bc/2. The last observation is the starting point for Veljan’s results in [2] and [3] that

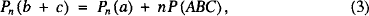
when the angle A is π - 2π/n radians and that

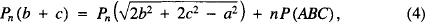
when the angle A is 2π/n radians.

Type
Research Article
Information
The Mathematical Gazette , Volume 84 , Issue 500 , July 2000 , pp. 260 - 264
Copyright
Copyright © The Mathematical Association 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Kovaöevic, Josip and Veljan, Darko, A triangular analogue of the Pythagorean theorem, Math. Gaz. 80 (November 1996), pp. 550–554.Google Scholar
2. Veljan, Darko, An analogue of the Pythagorean theorem with regular n-gons instead of squares, Elemente der Mathematik 51 (1996), pp. 156–160.Google Scholar
3. Veljan, Darko, Poopceni Pitagorin pouòak s pravilnim poligonima umjesto kvadratima, Matematiäko-fiziäki list 46 (1995/96), pp. 134–139.Google Scholar