No CrossRef data available.
Article contents
Repeated vector products
Published online by Cambridge University Press: 08 October 2020
Extract
In [1] the second author observed that it is possible to have a binary operation * on a set X with the property that two different arrangements of brackets in a given combination x1 * … * xn of elements of X yield the same outcome for all choices of the xj. For example, for the operation of subtraction on the set of real numbers, we have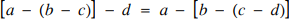 $$\left[ {a - \left( {b - c} \right)} \right] - d = a - \left[ {b - \left( {c - d} \right)} \right]$$
$$\left[ {a - \left( {b - c} \right)} \right] - d = a - \left[ {b - \left( {c - d} \right)} \right]$$
Information
- Type
- Articles
- Information
- Copyright
- © Mathematical Association 2020


