No CrossRef data available.
Article contents
Extract
The following method of introducing the ideas of rotation and strain into the study of Elasticity depends upon the identity
m · n grad u=n · (m grad u + m × curl u).....(1)
and upon the fact that if the straight line PQ undergoes a small rotation ω about an axis through P, the displacement of Q is
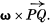
Consider first of all a rigid body which undergoes a small displacement. Let the point P of the body move to P′. We shall represent PP′ by u and regard u as typical of a vector field extending throughout the space originally occupied by the body. Let Q be a point near to P and represent 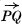 by m.
by m.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1941


