Article contents
Semi-magic squares and their orthogonal complements
Published online by Cambridge University Press: 01 August 2016
Extract
Not long ago I came across the following quiz in the Sunday supplement of the Spanish newspaper El País: Check that it does not matter how you take any four numbers from the following array; provided that no two of them lie in the same row or column, their sum is always the same.
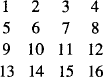
This reminded me of magic squares: square matrices where the sum of the elements in each line (row or column) and diagonal is always the same. Magic squares are a topic in recreational mathematics. Usually one looks for magic squares with elements that are integer, positive and different from each other, e.g. 1,2,…, n2 for a n × n as in
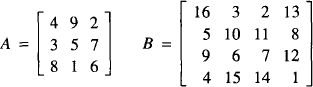
According to a Chinese legend, matrix A appeared engraved on the carapace of a turtle about 2000 BC. On the other hand, matrix B appears in Albrecht Dürer’s engraving Melencholia (1514) [1].
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 1996
References
- 3
- Cited by


