Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Öktem, I. Ferit
2015.
On the product .
The Mathematical Gazette,
Vol. 99,
Issue. 546,
p.
422.


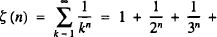
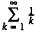 is divergent. A well-known particular value is ζ (2) = π
is divergent. A well-known particular value is ζ (2) = π