No CrossRef data available.
Article contents
A simple proof of Euler's continued fraction of e1/M
Published online by Cambridge University Press: 14 June 2016
Extract
A continued fraction is an expression of the form
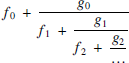
and we will denote it by the notation [f0, (g0, f1), (g1, f2), (g2, f3), … ]. If the numerators gi are all equal to 1 then we will use a shorter notation [f0, f1, f2, f3, … ]. A simple continued fraction is a continued fraction with all the gi coefficients equal to 1 and with all the fi coefficients positive integers except perhaps f0.
The finite continued fraction [f0, (g0, f1), (g1, f2),…, (gk–1, fk)] is called the k th convergent of the infinite continued fraction [f0, (g0, f1), (g1, f2),…]. We define
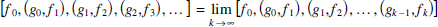
if this limit exists and in this case we say that the infinite continued fraction converges.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 2016
References
1.Euler, L., De fractionibus continuis dissertatio, Commentarii academiae scientiarum Petropolitanae 9 (1744) pp. 98–137 also available at http://eulerarchive.maa.org/pages/E071.htmlGoogle Scholar
2.Hermite, C., Sur la fonction exponentielle, Comptes rendus de l'Académie des sciences Paris (1873) pp. 18-24, pp. 74-79, pp. 226-233, pp. 285-293.Google Scholar
3.Olds, C. D., The simple continued fraction expansion of e, Amer. Math. Monthly 77 (1970) pp. 968–974.CrossRefGoogle Scholar
4.Cohn, H., A short proof of the simple continued fraction expansion of e, Amer. Math. Monthly 113 (2006) pp. 57–62.Google Scholar
5.Osler, T. J., A proof of the continued fraction expansion of e 1/M, Amer. Math. Monthly 113 (2006) pp. 62–66.Google Scholar
6.Borwein, J. M., van der Poorten, A. J., Shallit, J. O. and Zudilin, W., Neverending fractions: an introduction to continued fractions, Cambridge University Press (2014) pp. 45–49.CrossRefGoogle Scholar
7.Rose, H. E., A course in number theory (2nd edn.), Oxford University Press (1994) Excercises 15, 16, pp. 143-144.Google Scholar
8.Khrushchev, S., On Euler's differential methods for continued fractions, Electronic transactions on numerical analysis 25 (2006) pp. 178–200.Google Scholar

