No CrossRef data available.
Article contents
Some remarks about a formula of Charles Dodgson
Published online by Cambridge University Press: 23 January 2015
Extract
In this note we start by exploring a type of solution of the equation in positive integers
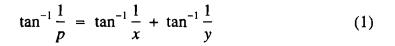
for a given p, which will enable us easily to derive a class of solutions in integers of the more general equation in positive integers

for any positive integers p and n.
In another part of this note we explore some connections between the formula we find and a particular chapter in the elementary theory of numbers.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2012
References
1.
Abeles, Francine F., Charles L. Dodgson's geometric approach to arctangent relations for pi, Historia Mathematica
20 (1993) pp. 151–159.CrossRefGoogle Scholar
2.
Wetherfield, Michael, The enhancement of Machin's formula by Todd's process, Math. Gaz.
80 (July 1996) pp. 333–344.CrossRefGoogle Scholar
3.
Wrench, J. W., The evolution of extended decimal approximation to π, The Mathematics Teacher, 53 (December 1960) pp. 644–650.Google Scholar
4.
Berggren, Lennart, Borwein, Jonathan and Borwein, Peter, Pi: A Source Book, Springer Verlag (1997).CrossRefGoogle Scholar
5.
Wetherfield, Michael and Chien-Lih, Hwang, Some new inverse cotangent identities for π, Math. Gaz.
81 (November 1997) pp. 459–460.Google Scholar
6.
Davenport, H., The higher arithmetic (5th edn.), Cambridge University Press (1982).Google Scholar
7.
Frink, Orrin, Almost Pythagorean triples, Mathematics Magazine
60 (October 1987) pp. 234–236.CrossRefGoogle Scholar
8.
Ore, Oystein, Number theory and its history, Dover Publications, Inc.
New York (1988).Google Scholar
9.
Bradley, C. J., On solutions of m2 + n2 = 1 + t2
, Math. Gaz.
80 (November 1996) pp. 404–406.CrossRefGoogle Scholar
10.
Bradley, C. J., From integer Lorentz transformation to Pythagoras, Math. Gaz.
88 (March 2004) pp. 16–21.CrossRefGoogle Scholar
11.
Dickson, Leonard E., Lowest integers representing sides of a right triangle, Am. Math. Monthly
1 (1894) pp. 6–11.CrossRefGoogle Scholar

