Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-14T07:28:00.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Trigonometric identities and functional equations

Published online by Cambridge University Press:  01 August 2016

Pl. Kannappan
Pl. Kannappan*
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1
Get access Rights & Permissions [Opens in a new window]

Extract

Dedicated to Professor S. Kurepa on the occasion of his 73rd birthday. We are familiar with many trigonometric formulas (identities)

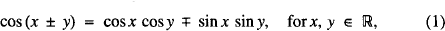
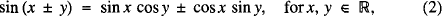
leading to five more identities

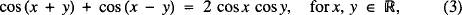
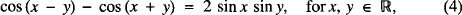
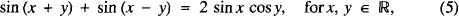
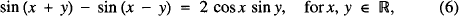
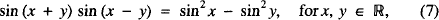
and so on, where #x211D; is the set of reals.

Type
Articles
Information
The Mathematical Gazette , Volume 88 , Issue 512 , July 2004 , pp. 249 - 257
Copyright
Copyright © The Mathematical Association 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. laBere, J. C. W. D., The addition theorem for circular and hyperbolic sine, Math. Gaz. 40 (1956) pp. 130–131.Google Scholar
2. Lunn, A. C., The foundations of trigonometry, Ann. Math. 10(2) (1908) pp. 37–45.Google Scholar
3. Naylor, V., Note on the nature of trigonometry, Math. Gaz. 17 (1933) pp. 316–318.CrossRefGoogle Scholar
4. Parameswaran, S., Trigonometry retold, Math. Gaz. 42(340) (1958) pp. 81–83.CrossRefGoogle Scholar
5. Aczel, J., Lectures on functional equations and their applications, Academic Press, New York (1966).Google Scholar
6. Aczel, J. and Dhombres, J., Functional equations in several variables, Cambridge University Press (1989).CrossRefGoogle Scholar
7. Kannappan, PL., Theory of functional equations, Mat. Science Report 48, Madras (1969).Google Scholar
8. d’Alembert, J., Mémoire sur les principes de mécanique, Hist. Acad. Sei. Paris (1769) pp. 278–286.Google Scholar
9. Kurepa, S., On the functional equation f(x + y) f(x - y) = f (x)2 - f(y)2 , Annales Polon. Math. 10 (1961) pp. 1–5.Google Scholar
10. Stephens, R., The sine and cosine functions, Math. Magazine 36 (1963) pp. 302–311.Google Scholar
11. Wilson, W.H., On certain related functional equations, Bull. Amer. Math. Soc. 26 (1919–1920) pp. 300–312.CrossRefGoogle Scholar
12. Wilson, W. H., Two general functional equations, Bull. Amer. Math. Soc. 31, (1925) pp. 330–334.Google Scholar
13. Kannappan, PL., The functional equation �(xy) +f(xy-l) = 2f(x)f(y) for groups, Proc. Amer. Math. Soc. 19 (1969) pp. 97–104.Google Scholar
14. Chung, J. K., Kannappan, PL. and Ng, C. T., A generalization of the cosine-sine functional equation on groups, Linear Algebra and its Applications 66 (1985) pp. 259–277.Google Scholar