Published online by Cambridge University Press: 15 June 2008
Previous work has shown that intracellular delay needs to be taken into account toaccurately determine the half-life of free virus from drug perturbation experiments [1]. The delayalso effects the estimated value for the infected T-cell loss rate when we assume that the drug isnot completely effective [19]. Models of virus infection that include intracellular delay are moreaccurate representations of the biological data.
We analyze a non-linear model of the human immunodeficiency virus (HIV) infection thatconsiders the interaction between a replicating virus, CD4+ T-cell and the cytotoxic-lymphocytes(CTL).We then investigate the intracellular delay effect on the stability of the endemically infectedsteady state. Criteria are given to ensure that the infected steady state is asymptotically stable forall delays. Model analysis also allows the prediction of a critical delay $\tau_c$ 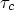 below which the effectorCTL can play a significant role in the immune control mechanism even when the basic reproductionnumber is high.
below which the effectorCTL can play a significant role in the immune control mechanism even when the basic reproductionnumber is high.