Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Miller, H. D.
1962.
A Matrix Factorization Problem in the Theory of Random Variables Defined on a Finite Markov Chain.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 58,
Issue. 2,
p.
268.
Presman, E. L.
1967.
Boundary Problems for Sums of Lattice Random Variables, Defined on a Finite Regular Markov Chain.
Theory of Probability & Its Applications,
Vol. 12,
Issue. 2,
p.
323.
Gani, J.
1969.
Recent advances in storage and flooding theory.
Advances in Applied Probability,
Vol. 1,
Issue. 1,
p.
90.
Gani, J.
1969.
Recent advances in storage and flooding theory.
Advances in Applied Probability,
Vol. 1,
Issue. 1,
p.
90.
Keilson, Julian
and
Rao, S. Subba
1970.
A process with chain dependent growth rate.
Journal of Applied Probability,
Vol. 7,
Issue. 3,
p.
699.
Keilson, Julian
and
Rao, S. Subba
1970.
A process with chain dependent growth rate.
Journal of Applied Probability,
Vol. 7,
Issue. 03,
p.
699.
�inlar, Erhan
1972.
Markov additive processes. I.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 24,
Issue. 2,
p.
85.
Arjas, E.
1972.
On a fundamental identity in the theory of semi-Markov processes.
Advances in Applied Probability,
Vol. 4,
Issue. 02,
p.
258.
Arjas, E.
1972.
On the use of a fundamental identity in the theory of semi-Markov queues.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
271.
Arjas, E.
1972.
On the use of a fundamental identity in the theory of semi-Markov queues.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
271.
Arjas, E.
1972.
On a fundamental identity in the theory of semi-Markov processes.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
258.
Newbould, M.
1973.
A classification of a random walk defined on a finite Markov chain.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 26,
Issue. 2,
p.
95.
Arjas, E.
and
Speed, T. P.
1973.
An extension of Cramér's estimate for the absorption probability of a random walk.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 73,
Issue. 2,
p.
355.
Takács, Lajos
1975.
A storage process by semi-Markov input.
Advances in Applied Probability,
Vol. 7,
Issue. 4,
p.
830.
Takács, Lajos
1975.
A storage process by semi-Markov input.
Advances in Applied Probability,
Vol. 7,
Issue. 4,
p.
830.
Tsui, E.
and
Wong, E.
1975.
A sequential approach to heart-beat interval classification (Corresp.).
IEEE Transactions on Information Theory,
Vol. 21,
Issue. 5,
p.
596.
Reinhard, J. M.
1981.
A semi-markovian game of economic survival.
Scandinavian Actuarial Journal,
Vol. 1981,
Issue. 1,
p.
23.
Arndt, K.
1981.
Asymptotic Properties of the Distribution of the Supremum of a Random Walk on a Markov Chain.
Theory of Probability & Its Applications,
Vol. 25,
Issue. 2,
p.
309.
Phatarfod, Revindra M.
1982.
On some applications of Wald's identity to dams.
Stochastic Processes and their Applications,
Vol. 13,
Issue. 3,
p.
279.
Janssen, Jacques
1982.
Stationary semi-Markov models in risk and queueing theories.
Scandinavian Actuarial Journal,
Vol. 1982,
Issue. 3-4,
p.
199.

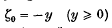
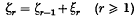
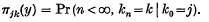
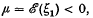 , the expectation of ξ
, the expectation of ξ