Published online by Cambridge University Press: 24 October 2008
An ‘inner measure’ analogous to Lebesgue inner measure and associated with a von Neumann algebra 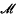 is constructed on the linear sets of a Hilbert space. We supposed
is constructed on the linear sets of a Hilbert space. We supposed 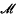 to be of finite type and countably decomposable, as these restrictions will be necessary for some of the results obtained. As remarked by Dye in (2), Type II1 algebras have a structure analogous to that of a finite non-atomic measure space, the trace corresponding to the measure. We define a class of ‘measurable sets’ and obtain some of its properties. The development of the theory is indicated also from the starting point of a function-valued dimension function. The idea for the construction of such an inner measure comes from a remark in (3), paragraph 16·2, and the terminology of (3) and of (5) is used throughout.
to be of finite type and countably decomposable, as these restrictions will be necessary for some of the results obtained. As remarked by Dye in (2), Type II1 algebras have a structure analogous to that of a finite non-atomic measure space, the trace corresponding to the measure. We define a class of ‘measurable sets’ and obtain some of its properties. The development of the theory is indicated also from the starting point of a function-valued dimension function. The idea for the construction of such an inner measure comes from a remark in (3), paragraph 16·2, and the terminology of (3) and of (5) is used throughout.